
This indicates information about where you are - the Given - and where you're going - what I call To Prove That.Īfter all, if you don't know ie.

Understand what you're Given and What You Need To Prove. Let subsequent Statements be written together like in a paragraph. You are expected to know both!īut relax if the latter variety is unfamiliar: simply write down your Statement (as you normally would), then say 'because', and write down your Reason. OR email me: Proofs can be written in Tabular Statement-Reason format OR in Free-flowing Paragraph form.
#WRITING PROOFS IN GEOMETRY HOW TO#
By the way, I knew how to prove it ordinarily too.!) (This might be pushing it a bit but for one of the Geometry Free Response Qs, I used Algebra II-level Trigonometry alone since it just seemed easier for me than 'conventional' Geometry.
#WRITING PROOFS IN GEOMETRY PROFESSIONAL#
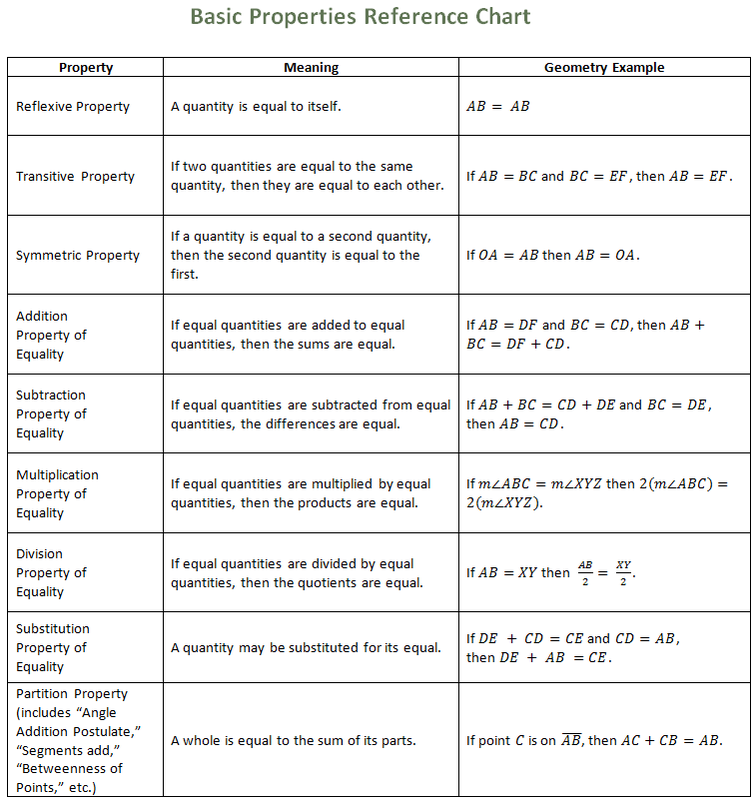
The CSET examiners are very competent and professional and will accept any Proof that appears reasonable! There is no one RIGHT way to prove a proposition, especially if it seems rather complicated! ANY method or approach that consists of logically linked Statements - that is, you don't SKIP a step! - supported by valid Reasons shall do splendidly. Here are general Tips about approaching and writing robust Geometric Proofs:ġ. And, obviously, this might be one you're familiar with, or something novel and challenging.īut proofs are actually quite simple once you realize that they follow a very definite 'system' or structure. Likewise, AT LEAST one Q in the Free Response section shall be a Proof. With regards to the CSET, you're sure to encounter at least a couple of Proofs in the MCQ section wherein you are expected to supply the missing step of a Proof by selecting the most relevant choice. Proofs require you to reason very logically and analytically - the deductive reasoning is of a high order! - and it calls for a peculiarly methodical approach not encountered elsewhere. The allergy of students against Proofs shouldn't be particularly surprising: many Geometry teachers themselves cower at the sight of an 'unfamiliar' Proof! Kids in schools HATE proofs universally (!), and I must say that teachers do their tuppence to cultivate such sentiments. One of the most challenging - and intimidating - aspect of Subtest II: Geometry, is writing Proofs for Geometric Propositions. How does one write robust Geometric Proofs?


 0 kommentar(er)
0 kommentar(er)
